Triangular Irregular Network (TIN) Models
These use a regular lattice to sample heights. The fineness or coarseness of the lattice may be varied to suit the variation in terrain. Nevertheless the sampling may miss abrupt changes in relief and there is, therefore, a tendency to smooth out features. The main advantage is reduced processing time and quick data capture. Figure 3 shows a surface modelled using a regular grid.
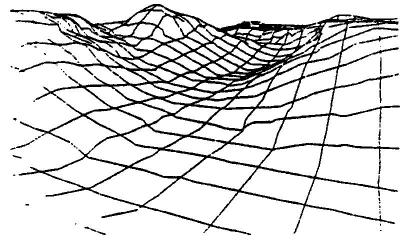
Figure 3. A surface modelled using a regular grid ( Mclaren and Kenny 1989) Triangular Irregular Networks use the sampled heights as nodes on a network. The lines joining the nodes form triangles, which are irregular in size, shape and orientation. The aim in fitting the triangles is to produce triangles that are equilateral and that have sides as short as possible. The triangles represent a facet in the topography of the area. A facet is an area of common slope and aspect. TIN models accept random height sampling, enabling samples to be closer together in areas with many relief features. They also accept break lines and hold spot height values for peaks and depressions. Break lines are natural features that triangles should not cross e.g. ridge lines, where they can be used to the top of a hill appearing as a flat plateau. TIN models, therefore, produce more triangles in areas of varied relief, thus capturing more of the relief patterns than grid models (Stocks and Heywood 1994). TIN models have the disadvantage of producing discontinuity of the surface at the triangle boundaries so that the resulting surface looks very angular (Gold 1989). Figure 4 shows a TIN model of the same surface shown in figure 3. Note the more angular nature of figure 4, but also note the greater detail in the landform shown in figure 4.
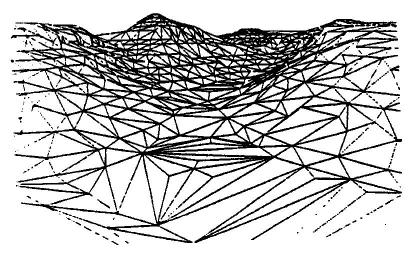
Figure 4. A surface modelled using a TIN (McLaren and Kenny 1989) Brunsdon and Carter (1993) experimented with the accuracy of terrain sampling strategies. They found that by selecting only very important points (VIP sampling) on a surface the number of sampling points could be reduced by more than 90% without a great reduction in the accuracy of the DEM. Their experiment, however, relied on the construction of a DEM from a set of sample points and then the application of a VIP algorithm to select a subset of points that best described the surface. This approach does not offer a means of reducing the initial set of sampling points or of defining which are the best points to describe a surface for which a DEM has not been built.